Introduction to Maxima – A Computer Algebra System

電腦代數系統Maxima 的簡介

　

1968~1982年美國M.I.T. 發展了電腦軟體 Macsyma, 是第一個可以處理數學符號運算的人工智慧軟體.  它是現代符號運算軟體的鼻祖, 現今這類統稱為電腦代數系統 (Computer Algebra System); 後來, 演化成自由軟體 Maxima.

 

免費的常用電腦代數系統還有 Axiom, Sage 等幾種. 目前在台灣流行的商業數學符號運算軟體, 主要是 Maple 和 Mathematica 兩種. 此類軟體的比較, 可參考維基百科的說明.

　

http://en.wikipedia.org/wiki/Comparison_of_computer_algebra_systems

 

相對於符號運算軟體的是另一種稱為數值計算環境 (Numerical Computing Environment) 的軟體. 最具代表性的就是商業軟體 MATLAB. 與 其功能相近但免費的軟體首推 Scilab. 統計常用且免費的數值計算環境以 R Language 最廣受使用.

　

      http://en.wikipedia.org/wiki/List_of_numerical_analysis_software


　


　

Introduction to wxXMaxima (圖形化介面的 Maxima )

　

　

     Maxima 有三種工作方式: wxMaxima, XMaxima, 及 DOS 環境. 這裡只介紹最容易上手的 wxMaxima.

　

一.  如何啟動 wxMaxima

　

       從桌面啟動 wxMaxima 或使用開始與程式的功能表啟動, 就可以看到下列畫面.

　

　

　

　

 二. wxMaxima  操作簡介

　

    1.  啟動常用數學指令窗格, 以利操作.

           

 

 

 

 

　

　

　

　

　

　

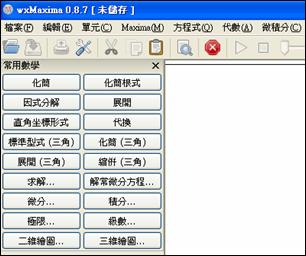   螢幕左邊會出現常用數學指令窗格:

     

　

　

　

　

在學會使用這些指令前, 必須知道
如何輸入數學運算式, 請參考下一項說明.

   

　

　

　

　

　

　

　

　

　

　

　

  2.  數學運算式輸入的注意事項:

　

　

        加減乘除的符號分別為    +   -   *  /, 而次方的符號是 ^

　

         x 的 3 次方, 輸入方式為     x^3

　

        函數 sin x, log x 等, 必須使用小括號, 如 sin(x)  , log(x).  

　

         %pi 代表圓周率, %e 是 Euler's number (), %i = , %alpha 代表 .

　

        另外, 單獨的百分比符號 % 則是代表前一個運算的結果.

　

　

     3. 指令執行: 有三種方式執行指令.

        

              (1) 點選指令窗格.

　

            (2) 在輸入單元(參考下一個說明)直接輸入指令後, 按 Ctrl + Enter 來執行.

　

              (3) 結合前兩種方式 

　

　

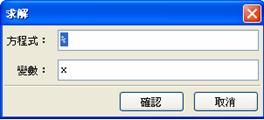
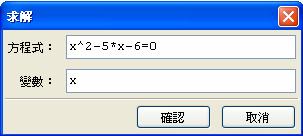
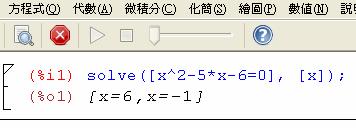
例: 點選指令窗格執行求解方程式  , 操作方式如下:

　

　

　

                                                 

 

 

    

 

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

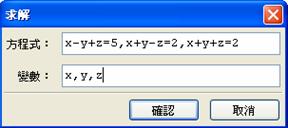
   備註: 如果要解聯立方程式, 可以這樣輸入: 

 

 

　

　

　

　

　

　

　

4.      輸入單元執行方式: 

 

(1)   選取 Cell 底下的 Insert Input Cell 或直接按 F5, 會出現輸入單元. 

 

      

    

 

 

 

 

　

　

　

　

　

　

　

　

　

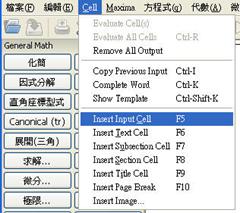
(2)   輸入運算式後, 再按 <Ctrl>+<Enter> 就可以執行運算. 如

 

　

　

　

  展開

　

　

              因式分解

　

　

            求解

　

　

            繪圖

　

　

　

　

　

                備註: 在輸入單元內藍色字是輸入的運算式, 黑色字則是運算的結果.

   


　

5.  繪圖

　

        (1) 指令    plot2d (sin(x), [x, -5, 5]);      就可繪出 sin x 在[-5, 5] 之間的曲線.

　

        (2) 下列指令的例子是使用 200 個點來描繪參數曲線   x = t - sin t,  y = 1 - cos t

　

             plot2d( [parametric, t-sin(t), 1-cos(t), [ t, 0, %pi*4 ], [nticks, 200] ], [x,-1,8],[y,0,3] ) ;

　

             註:  nticks 意指描繪畫該曲線時,使用點總數的選項.

　

 

三.    Maxima 指令的基本語法: 就是在輸入單元內使用運算式的語法

　

      基本語法:  每一行 Maxima 敘述須以 ; 作結尾, 依執行效果可分

　

         (1)  Maxima 指令式: 執行計算,繪圖,求解等 Maxima 指令.

　

                         語法:       <Maxima 指令> ;    例如,

　

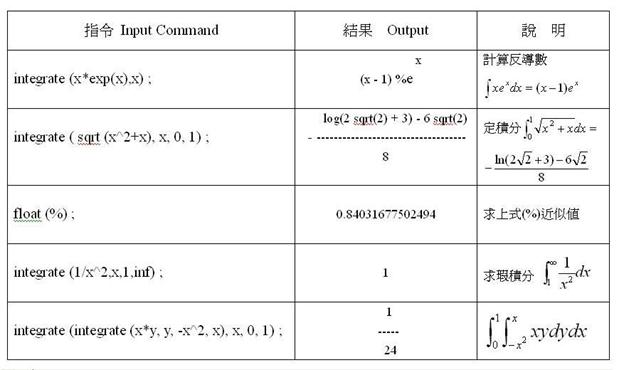
                                    integrate (x * exp(x), x) ;           - 求不定積分

　

                                    factor ( x^2 - 3*x + 2) ;             - 因式分解

　

                          若沒輸入分號 ;  就按 <Enter>, 則指令不會執行. 此時可補輸入再執行.

　

                          若結尾以符號 $ 取代分號 ; 則計算值不會出現在螢幕上

　

           (2)  指定式: 指定變數的代表值, 代表式, 或方程式等運算式.

　

                             語法        <變數名稱 > : <運算式 exp> ;

　

                             例如,       

　

                    a : 10 ;                                       - 將符號 a 指定為 10

                

                                    b : x^2 - x ;                                - 符號 b 代表  x^2 - x

                        

                            符號:  四則運算( +, -, *, /), 次方 (^), 自然對數 ( log ), 指數函數 exp (x)

　

       (3) 定義函數

　

                            語法:    <函數名稱> ( <變數1>, <變數2>, ... ) : =  <運算式>

　

                            例如: 

　

                                         f(x) := x^2 - 2*x + 3;

　

                                         g(x,y) := x*y*exp(-x^2-y^2);

　

　

  四. 常用的微積分指令:

 

                   limit (x/sin(x), x, 0, plus);                    -   

　

                   limit ((x^2-3)/(2*x^2+x-5), x, inf);      -     inf 指無窮大 (minf指 minus infinity)

　

                   diff (tan(x)*cosh(x), x);                       -     tan x cosh x 對 x 取導數

　

                   diff (sin(x^2), x, 2);                              -     微分兩次

　

　

　

 五. 繪圖指令介紹

　

            (a)  單一自變數函數圖形

　

                    plot2d (exp(-x^2), [x, -3, 3], [y, 0, 2]);

 
                     
    


　

　

　

　

　

　

　

　

　

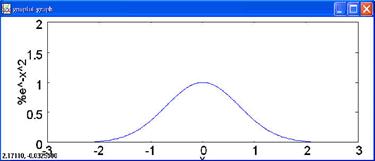
           (b) 兩個自變數的函數圖形

 

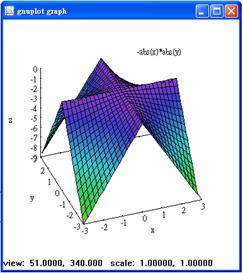                  plot3d (-abs(x*y),[x,-3, 3], [y, -3, 3]);

 

　

　

                 用滑鼠點選圖形後,可以藉著拖曳滑鼠
　

                 來改變觀測圖形的角度.

 

 

 

　

　

　

　

           (c) 方程式的繪圖與極座標的繪圖.

　

　

　

XMaxima 畫圖指令

指令說明或結果

load ( implicit_plot ) $

implicit_plot ([ x^2+y^2=1, x^2-y^2=1],

[x,-2,2], [y,-2,2],

[gnuplot_preamble, "set zeroaxis"]);


畫方程式的圖形 ,  
 .

load (draw) $
draw2d ( nticks = 200,

polar( cos(2*theta), theta, 0, 2*%pi) )$

四葉玫瑰線
畫極座標表示的函數曲線圖形

draw2d (nticks = 400,

polar( sin (8*theta/5), theta, 0, 10*%pi) )$

畫極座標表示的函數曲線圖形
用 400 個點描繪曲線.

draw3d ( implicit (x^2+y^2-z^2=1,

        x, -5, 5, y, -5, 5, z, -2, 2),

               surface_hide = true) $

畫三維方程式的曲面圖

contour_plot (4*x^2 + y^2, [x, -10, 10], [y, -10, 10]);

畫等值線(等高線)

 

　

        備註: 使用 draw2d 和 draw3d 的任一指令前, 都必須先執行 load(draw)$.


　

六. 動畫.

 

    with_slider 使用 plot2d 畫圖.

 

    動畫例一: 移動的正弦函數曲線.

 

(1) 首先使用指令繪圖

　

with_slider ( n, [1,2,3,4,5,6], sin( x – n * %pi / 3 ), [x, -6, 6], [y, -2, 2] )$

　

　

 

      (2)用滑鼠選取圖後, 接著點選上方功能表的三角形來啟動播放功能

　

 

      

 

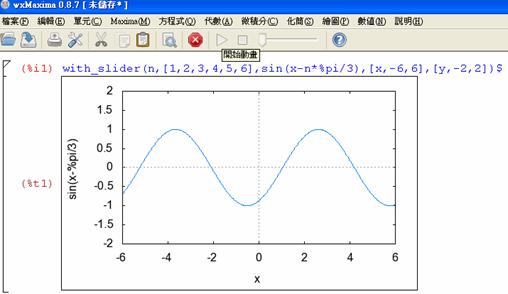
         說明:

               n 是變動值, 從 1 變動至 6.  因為 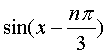   的曲線是  往右移動 ,

　

               所以 n = 1, 2, 3, 4, 5, 6 六張圖連續播放, 就造成了曲線往右方連續移動的動畫.

 


　

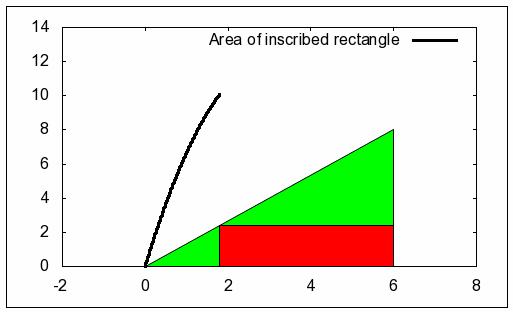
  動畫例二:  修改自http://wxmaxima.sourceforge.net/wiki/index.php/Animations

 

        load (draw);

　

with_slider_draw ( b, makelist (i, i, 0, 30)/5, color = black,

fill_color = green, polygon ( [ [0,0], [6,0], [6,8] ] ),

fill_color = red,  polygon ( [ [b, 0], [6, 0], [6, 4*b/3], [b, 4*b/3] ]),

line_width = 3, key = "Area of inscribed rectangle",

　

       explicit ( 4 * x / 3 * (6-x), x, 0, b), yrange = [0, 14], xrange = [-2, 8] ) $