Introduction to XMaxima

     Maxima 有三種工作環境: XMaxima, wxMaxima, 及 DOS 環境.

    一.  如何啟動 XMaxima

    二.  XMaxima 指令簡介

           1. 基本語法

           2. 微積分

           3.  繪圖

           4. 基本數學

           5. 微分方程

一.  如何啟動 XMaxima

     1. 從桌面啟動 XMaxima 或使用開始與所有程式的功能表啟動, 就可以看到下列畫面.

     2.  將游標移到 (%i1) 後, 就可以開始輸入 Maxima 的數學指令.  如輸入

                integrate(x*log(x),x);    

          再按 <Enter> 鍵, 就可以執行下列不定積分式的計算

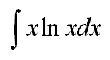
          注意:

              (a)  指令的最後有分號 ";".

              (b)  在 Maxima 中, 自然對數函數  ln x  是用 log (x) 表式.

     3. 如果輸入指令                                                                    

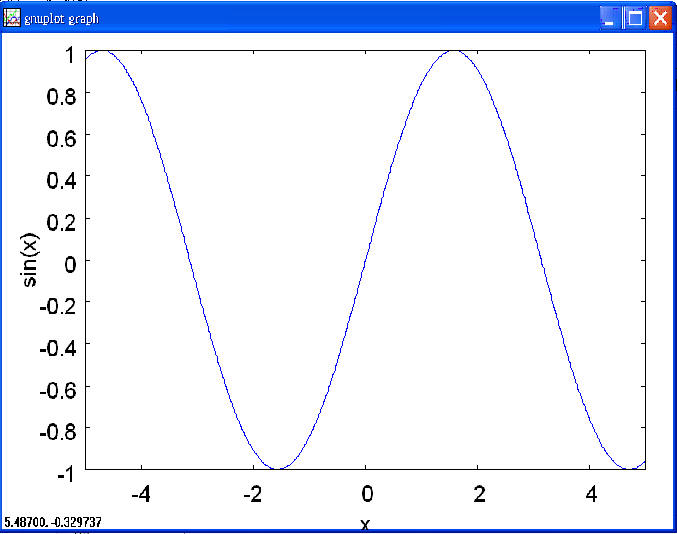
                               plot2d (sin(x), [x, -5, 5]);     

         就可繪出 sin x 在[-5, 5] 之間的曲線.

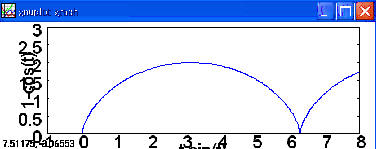
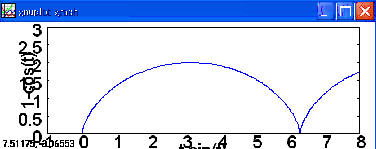
     4. 下列指令的例子是使用 200 個點來描繪參數曲線

                    x = t - sin t

                 y = 1 - cos t

        plot2d ([parametric, t-sin(t), 1-cos(t), [t,0,%pi*4],[nticks, 200]], [x,-1,8],[y,0,3]);

        註:  nticks 意指描繪畫該曲線時,使用點總數的選項.

 二. XMaxima 指令簡介

          1. 基本語法:  每一行 Maxima 敘述須以 ; 作結尾, 依執行效果可分

                  (1)  Maxima 指令式: 執行計算,繪圖,求解等 Maxima 指令.

                          語法:       <Maxima 指令> ; 

                          例如,

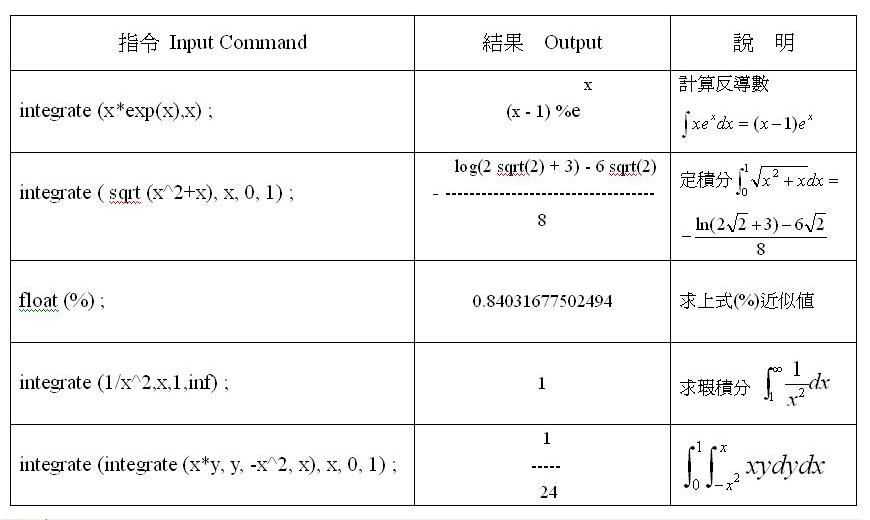
                                     integrate (x * exp(x), x) ;           - 求不定積分

                                     factor ( x^2 - 3*x + 2) ;             - 因式分解

                          若沒輸入分號 ;  就按 <Enter>, 則指令不會執行.
                          此時可再按 ;  <Enter> 就可執行指令.

                          若結尾以符號 $ 取代分號 ; 則計算值不會出現在螢幕上

                  (2)  指定式: 指定變數的代表值, 代表式, 或方程式等運算式.

                         語法        <變數名稱 > : <運算式 exp> ;

                         例如,

                                    a : 10 ;                                       - 將符號 a 指定為 10

                                    b : x^2 - x ;                                - 符號 b 代表  x^2 - x

                         運算符號:  四則運算( +, -, *, /), 次方 (^), 自然對數 ( log ), 指數函數 exp (x)

                  (3) 定義函數

                        語法:    <函數名稱> ( <變數1>, <變數2>, ... ) : =  <運算式>

                        例如: 

                                     f(x) := x^2 - 2*x + 3;

                                     g(x,y) := x*y*exp(-x^2-y^2);

          2. 微積分指令:

               範例:

                      limit (x/sin(x), x, 0, plus);                    -   

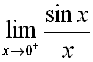
                      limit ((x^2-3)/(2*x^2+x-5), x, inf);      -     inf 指無窮大 (minf指 minus infinity)

                      diff (tan(x)*cosh(x), x);                      -     tan x cosh x 對 x 取導數

                      diff (sin(x^2), x, 2);                             -     微分兩次

           3. 繪圖

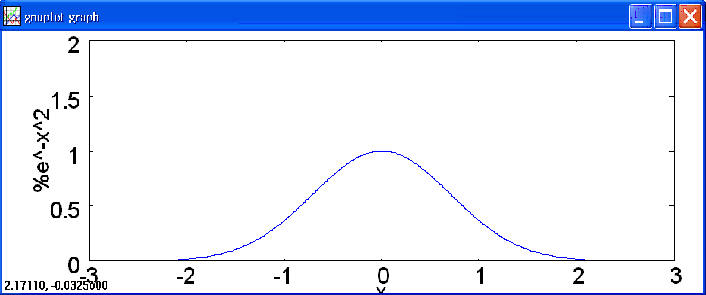
                (a)  單一自變數函數圖形

                       plot2d (exp(-x^2), [x, -3, 3], [y, 0, 2]);

                (b) 兩個自變數的函數圖形 (→)

                          plot3d (-abs(x*y),[x,-3, 3], [y, -3, 3]);

                (c) 參數曲線: 下列指令的例子是使用 200 個點來描繪參數曲線

                        x = t - sin t

                     y = 1 - cos t

          plot2d ([parametric, t-sin(t), 1-cos(t), [t,0,%pi*4],[nticks, 200]], [x,-1,8],[y,0,3]);

                     註:  nticks 意指描繪畫該曲線時,使用點總數的選項. %pi 代表圓周率.

                (c)

           4. 基本數學

           5. 微分方程